John Tsang

John Tsang

A statistics graduate student in survey sampling.

An Example to Accelerate R with Rcpp and OpenMP: a Simulation Study of Survey with Systematic Non-responses

5 minute read

Result: Using Rcpp with OpenMP can accelerate the simulation about 70 times in R.

This note uses a simple simulation study1 as an example to show that using Rcpp with OpenMP can significantly accelerate computation in R. The simulation illustrates biases arising from systematic unit non-responses. Specifically, I study biases in

  • estimates of regression coefficients,
  • the Horvitz-Thompson (HT) estimator and
  • the variance estimator of the HT estimator.

Simulation

Simulation Setup

1. Population Generation

A bivariate fixed population \((X, Y)\) of size \(N = 1000\) comes from the following procedures:

  • Generate the covariate \(X\) from \(U[0, 4]\).
  • Generate the disturbance term \(e\) from \(N(0,1)\).
  • The survey response variable \(Y = 1 + 2X + e\).

If a unit satisfy the condition \(-1 < y - x - 2 < 1\), then this unit is a response. Otherwise, the unit is a non-response.

The R code for generating the fixed population:

set.seed(123456)
N = 1000
x = runif(N, 0, 4)
e = rnorm(N, 0, 1)
y = 1 + 2*x + e

The R code to generate a vector of indices of responses.

tmp = y - x - 2
pop.response.index = which((tmp > -1) & (tmp < 1))

The response rate is about 40%.

2. Simulation Procedure

Repeat the following two steps \(R = 1000\) times.

  1. Draw a 10%-sample (size \(n = 100\)) from the fixed population according to simple random sampling without replacement (SRSWOR).

  2. Ignoring non-responses, I use only response units to

    • fit a simple linear regression and record the two estimated coefficients,
    • calculate the HT estimator ,
    • estimate the variance of the HT estimator and
    • record the number of responses.

Using these recorded statistics, I calculate the Monte-Carlo relative biases and the Monte-Carlo number of responses.

Simulation Results

The following data table summarize simulation results.

                     Full Response Non-response
rel.bias.intercept            6.33         71.4
rel.bias.slope               -1.51        -37.4
rel.bias.HT.mean            0.0268        -30.7
rel.bias.var.HT.mean        0.0932        -37.3
num.response                   100         40.2

Simulation Results:
If non-responses are ignored, the non-response biases are huge for estimated regression coefficients (intercept and slope), the HT estimator and the estimator of the variance of the HT estimator.

Simulation Programs

R only

  • Variables setup: 
    n = 100
population = list(
intercept = 1,
slope     = 2,
mean      = mean(y),
var       = (1 - n/N) * var(y) / n
)
non.response = list(
intercept       = numeric(length=R),
slope           = numeric(length=R),
HT.mean         = numeric(length=R),
var.HT.mean     = numeric(length=R),
num.response    = numeric(length=R)
)
  • Helper function to record statistics from each replication: 
    SRSWOR = function(r, sample.x, sample.y, rt.lst) {
  model = lm(formula = "sample.y ~ sample.x")
  rt.lst$intercept[r] = as.numeric(model$coefficients[1])
  rt.lst$slope[r] = as.numeric(model$coefficients[2])
  rt.lst$HT.mean[r] = mean(sample.y)
  rt.lst$var.HT.mean[r] = (1 - length(sample.y)/N) * var(sample.y) / length(sample.y)
  rt.lst$num.response[r] = length(sample.y)
	
  return(rt.lst)
}
  • Helper function to calculate Monte-Carlo statistics from the simulation: 
    cal.statistics = function(lst) {
  rel.bias.intercept = (mean(lst$intercept) - population$intercept) / population$intercept * 100
  rel.bias.slope = (mean(lst$slope) - population$slope) / population$slope * 100
  rel.bias.HT.mean = (mean(lst$HT.mean) - population$mean) / population$mean * 100
  rel.bias.var.HT.mean = (mean(lst$var.HT.mean) - population$var) / population$var * 100
  num.response = mean(lst$num.response)
  rt.lst = list(
      rel.bias.intercept = rel.bias.intercept,
      rel.bias.slope     = rel.bias.slope,
      rel.bias.HT.mean   = rel.bias.HT.mean,
      rel.bias.var.HT.mean = rel.bias.var.HT.mean,
      num.response = num.response)
  return(rt.lst)
}
  • The function to run the simulation: 
    r.sim = function(R = 1000) {
  for (r in 1:R) {
      sample.index = sample(index, size = n, replace = FALSE)
    
      # SRSWOR with non-response
      sample.response.index = intersect(pop.response.index, sample.index)
      sample.y = y[sample.response.index]
      sample.x = x[sample.response.index]
      non.response = SRSWOR(r, sample.x, sample.y, non.response)
  }
  non.response.stat = cal.statistics(non.response)
  return(non.response.stat)
}

Rcpp

  • The C++ function for simulation in the source file simulation.cpp: 
    // [[Rcpp::export()]]
Rcpp::List simulation(const unsigned int R,
                      const unsigned int sample_size,
                      arma::vec y, arma::vec x,
                      arma::uvec response_index) {
  // WARNING: indices for arrays in C++ starts from 0,
  //          but those in R starts from 1
  response_index = response_index - 1;
  const unsigned int N = y.n_rows;

  Simulation_results s(R, N, arma::mean(y));
	
  for (unsigned int r = 0; r < R; ++r) {
      arma::uvec sample_index = arma::randperm<arma::uvec>(N, sample_size);
      arma::uvec sample_response_index = arma::intersect(response_index, sample_index);
      arma::vec sample_y = y.elem(sample_response_index);
      arma::vec sample_x = x.elem(sample_response_index);
      s.simulation(r, sample_x, sample_y);
  }
  s.compute_results();
	
  return Rcpp::List::create(
    Rcpp::_["intercept"] = s.MC_intercept,
    Rcpp::_["slope"] = s.MC_slope,
    Rcpp::_["HT.mean"] = s.MC_HT_mean,
    Rcpp::_["var.HT.mean"] = s.MC_var_HT_mean,
    Rcpp::_["num.response"] = s.MC_num_response
  );
}

    Download the full c++ source file simulation.cpp.

  • We load the library Rcpp and the C++ source file in R. 
    library(Rcpp)
sourceCpp("simulation.cpp")

Rcpp with OpenMP

  • Usually, when we run a program, the program is executed line by line (squentially). The above two (R only and Rcpp) are sequential programs.

  • Because each simulation replication does not affect the other, running iterations simultaneously instead of sequentially does not change the simulation outcome. Therefore, I use OpenMP to assign each computer processor to run simulation replications in parallel to save computation time. This type of programming is called parallel programming.

  • The exhibit below explains the shorter runtime when using OpenMP2.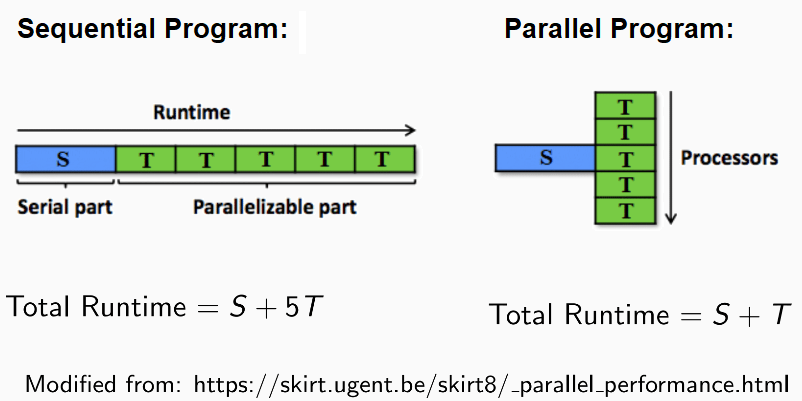 sequential-parallel.png
  • The C++ function for simulation in the source file simulation.cpp uses 5 processors at the same time: 
    // [[Rcpp::export()]]
Rcpp::List simulation_p(const unsigned int R, 
                      const unsigned int sample_size, 
                      arma::vec y, arma::vec x,
                      arma::uvec response_index) {
  // WARNING: indices for arrays in C++ starts from 0,
  //          but those in R starts from 1
  response_index = response_index - 1;
  const unsigned int N = y.n_rows;
  Simulation_results s(R, N, arma::mean(y));
	
  omp_set_num_threads(5);
  
  # pragma omp parallel for
  for (unsigned int r = 0; r < R; ++r) {
      arma::uvec sample_index = arma::randperm<arma::uvec>(N, sample_size);
      arma::uvec sample_response_index = arma::intersect(response_index, sample_index);
      arma::vec sample_y = y.elem(sample_response_index);
      arma::vec sample_x = x.elem(sample_response_index);
      s.simulation(r, sample_x, sample_y);
  }
  s.compute_results();

  return Rcpp::List::create(
    Rcpp::_["intercept"] = s.MC_intercept,
    Rcpp::_["slope"] = s.MC_slope,
    Rcpp::_["HT.mean"] = s.MC_HT_mean,
    Rcpp::_["var.HT.mean"] = s.MC_var_HT_mean,
    Rcpp::_["num.response"] = s.MC_num_response
  );
}

    Download the full c++ source file simulation.cpp.

  • We load the library Rcpp and the C++ source file in R. 
    library(Rcpp)
Sys.setenv("PKG_CXXFLAGS" = "-fopenmp")
Sys.setenv("PKG_LIBS" = "-fopenmp")
sourceCpp("simulation.cpp")

    The two lines Sys.setenv("PKG_CXXFLAGS" = "-fopenmp") and Sys.setenv("PKG_LIBS" = "-fopenmp") are to flag the use of OpenMP for the g++ compiler.

R Vs. Rcpp Vs. Rcpp with OpenMP: Rcpp with OpenMP Fastest

  • Runtime comparison: 
    library(microbenchmark)
microbenchmark(
r = {r.sim()},
rcpp = {simulation(R = 1000, sample_size = 100, 
                y = y, x = x,
                response_index = pop.response.index)},
rcpp2 = {simulation_p(R = 1000, sample_size = 100, 
                y = y, x = x,
                response_index = pop.response.index)},
times = 100L
)

    Output:

    Unit: milliseconds
expr      min         lq       mean     median         uq       max neval
   r 993.5976 1087.29510 1250.67629 1159.58185 1393.59430 2131.4919   100
rcpp  45.5461   48.05155   51.66997   51.06960   53.92465   67.7078   100
 rcpp2  24.2971   25.74590   26.57889   26.39155   27.18675   31.1330   100

    Result: Using Rcpp with OpenMP can accelerate the simulation about 70 (\(2131.4919 / 31.1330 \approx 68.5\)) times in R.

Footnote

  1. The simulation setup comes from Yap (2020). ↩

  2. The OpenMP supports shared-memory multi-platform parallel programming in Fortran, C and C++. For details, refer to the official page for OpenMP. ↩

You may also enjoy

The R6 Class in R

3 minute read

What is a class system? R is an object-oriented programming language with four object-oriented class systems.1 In other words, there are four ways to write ...